-
딥러닝 #3 생성모델 part 1 Boltzmann Machine인공지능 2021. 3. 8. 04:04
"
이전 글에서 합성 신경망에 대해 다루었다.
이번 글에서는 학습한 데이터와 유사한 데이터를 생성하는 생성모델에 대해 논하겠다. 통계물리학 개념을 활용하여 물질이 특정 형상(configuration)의 상태에 있을 확률을 표현하는 볼츠만 머신과 파생모델, 생성모듈&판별모듈 구조를 통해 데이터를 생성하는 GAN (Generative Adversarial Network, 대립쌍 생성망)을 다룰 것이다.
"생성모델
DNN 모델은 두 가지로 분류된다. 입력이 주어졌을 때 출력값을 결정하는 판별모델과, 특정 분포의 데이터가 만들어질 때 사용되는 함수나 절차를 모사하는 생성모델이 있다. 생성모델은 학습 데이터를 가장 잘 표현하는 확률분포를 출력으로 가진다.

입력과 출력에 대한 결합확률 분포 학습데이터에 대한 결합확률분포를 활용하여 조건부확률 p( y | x )를 계산, 분류나 회귀 문제를 해결하거나, 입력 x에 대한 결합확률분포 p(x)를 출력하여 군집화 문제를 해결하는 용도로 쓰인다. part 1에서는 대표적인 확률적 모델인 볼츠만 머신과 파생모델인 RBM(Restricted Boltzmann Machine),DBN(Deep belief Network)에 대해 논하겠다.
볼츠만 머신 (Boltzmann Machine)
볼츠만 머신은 통계물리학의 에너지 개념을 도입한 마르코프 모델의 일종으로, 에너지와 확률의 은유 관게를 활용하여 노드들이 가질 수 있는 값들의 집합에 대한 확률분포를 정의한 신경 모델이다. 은닉층과 가시층으로 나누어진 노드와 노드 사이를 잇는 간선으로 구성되어있으며, 노드들이 갖는 값들의 각 조합을 형상(미시적 상태)이라 하며, 형상 S에 대한 확률 P(S)를 에너지에 대해 다음과 같이 정의한 모델이다.

형상 S에 대한 확률 P(S), Z는 분할함수로 확률의 값이 1이 되도록 정규화하는 식이다. 
볼츠만 머신의 에너지 정의. 노드값이 확률적으로 정해지는 확률그래프 모델이다. 
볼츠만 머신의 구조 v와 h는 각각 입력과 출력(히든노드의 값), t_ij,r_ij 항은 각각 은닉층 노드, 가시층 노드 간의 가중치고 w_ij는 은닉층과 가시층 사이의 노드 간의 가중치다. a_i,b_j는 가시노드와 은닉노드의 편차항을 의미한다.
제한적 볼츠만 머신 (Restricted Boltzmann Machine)
은닉층간, 가시층간 노드의 가중치를 0으로 설정하면 제한적 볼츠만 머신이 된다. 제한적 볼츠만 머신은 더 깊은 신경망을 갖고, 가시 유닛이 관찰되고 고정되었을 때 은닉 유닛을 추론하는 마르코프 연쇄 몬테카를로 방법 (MCMC) 과정이 단 한번에 끝난다는 이점이 있다. 이 모델은 심층신뢰망 (DBN, Deep Belief Network)의 기본 뼈대가 된다.

제한적 볼츠만 머신의 활성화 함수. 해시넷 (hash.kr)참고 (태그2) 
제한적 볼츠만 머신의 구조 
제한적 볼츠만 머신의 에너지 정의. 은닉층간, 가시층간 가중치가 존재하지 않는다. 확률그래프의 추론과 재구성
RBM이 표현하는 확률 분포 - 문제에 주어진 정보를 해당노드의 입력값으로 설정한 다음 관심 대상인 노드들의 확률분포를 계산해 내는 것 - 을 확률 그래프의 추론이라 한다. 예를 들어 특정 언어를 모델링할 경우 어떤 음소 혹은 단어가 자주 등장하는지에 대한 분포 정보를 필요로 한다. 이는 RBM이 학습한 입력 데이터에 따라 결정되고 이를 통해 입력 데이터를 재구성할 수 있게 된다. 재구성은 입력 데이터의 확률 분포를 추정하는 과정으로, 특정 출력을 이끌어내는 회귀나 분류와는 다르다고 할 수 있다. 은닉노드의 값을 가중치를 이용해 입력노드에 전달하고, 입력값에서는 학습한 입력값을 전달받은 은닉노드 값과 bias를 더해 재구성하게 된다.
이를 수학적으로 접근하면 다음과 같다. RBM이 표현하는 결합확률 분포와 가시층이 특정 데이터 v (0 또는 1)을 가질 확률을 조합하여, 가시층값에 대한 은닉층 값의 확률을 유도한다.
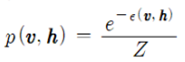
RBM이 표현하는 결합확률 분포 
가시층이 특정 데이터 v를 가질 확률 
가시층값이 'v'일때 은닉층값이 'h'일 조건부 확률 
v가 특정 값일 때 h가 1일 확률. 제한적 볼츠만 머신의 에너지 분포 정의와 조건부확률을 이용하여 유도하였다. 위 식은 입력데이터로 은닉층 값을 추정해가는 과정이다.

마찬가지로, h가 특정 값일때 v가 1일 확률. 입력데이터값을 추정하는 재구성 과정이다. RBM의 학습
RBM의 학습은 앞서 설명한 재구성과 가중치 수정 두 과정으로 구성된다. 위 학습의 목적은 학습데이터에 대해 높은 확률을 갖도록, 즉 학습데이터를 가장 유사하게 재구성할 수 있는 모델이 되도록 하는 것이다. 따라서 우리는 목적함수를
'가능도'라는 개념으로 설명할 것이다. 가능도란 RBM과 같은 확률 모델을 사용하여 계산한 데이터에 대한 확률, 즉 입력모델의 재현 정도를 의미하는데, 학습데이터를 가장 유사하게 재구성하기 위해서는 가능도를 최대로 만드는 파라미터를 선택해야 할 것이다. 따라서 학습방법은 경사 상승법으로 수행된다.

목적함수 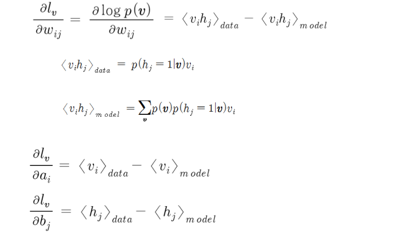
각 편미분 과정. 모델로부터 얻어지는 가시층 확률분포 -p(v)- 는 계산량이 매우 많다. 모델로부터 얻어지는 가시노드와 은닉노드 값 <Vi,Hi>model은 p(v)의 계산량이 매우 많기에 마르코프 체인 몬테카를로 추정이라는 기대값 추정 방법으로 계산량을 줄인다. 이 방법과 학습 알고리즘, 파생 모델 등은 part 2에서 자세히 다루도록 하겠다.
'인공지능' 카테고리의 다른 글
딥러닝 #2 (CNN 구조, CNN 학습 알고리즘) (1) 2021.02.17 딥러닝 #1 (작동 구조, 기울기 소멸 문제, 과적합 문제) (0) 2021.01.31 서포트 벡터 머신(Support Vector Machine) (0) 2020.12.20